Home > Press > A four-dimensional picture of our three-dimensional world
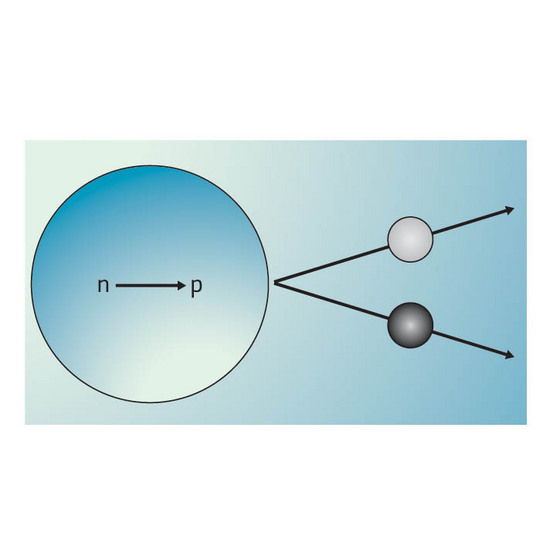 |
| Figure 1: In nuclear beta decay, a neutron (blue sphere) emits an electron (light grey) and a massless particle called a neutrino (dark grey). In so doing, the neutron turns into a proton. |
Abstract:
Scientists use a theory that exists in higher dimensions to better understand the process by which a neutron decays into a proton
A four-dimensional picture of our three-dimensional world
Japan | Posted on September 25th, 2008An international team of scientists from RIKEN at Brookhaven National Laboratory (BNL) and elsewhere in the USA, Japan and the UK are testing the Standard Model—the foundation of high-energy physics that unifies three of the four known forces found in nature—by calculating a well-known nuclear decay process1.
Summarizing the work, Thomas Blum, a member of the team, says: "We want to understand the structure of the particles in the nucleus from the standpoint of the Standard Model, in general, and quantum-chromodynamics (QCD), in particular. QCD is the theoretical basis for the strong force between quarks, the particles that make up neutrons, protons and other particles that are the building blocks of matter in our universe."
Most of the predictions of the Standard Model, which was developed in the 1960s, can only be tested at high-energy particle accelerators, such as CERN in Switzerland, or the Relativistic Heavy Ion Collider (RHIC) at BNL in the USA. In contrast, beta decay in radioactive nuclei is a well-known process that can be measured, extremely accurately, with a simple experimental set-up. Beta-decay occurs when a neutron emits an electron and a massless particle called a neutrino (Fig. 1). In so doing, the neutron turns into a proton.
Blum and colleagues calculated the part of the decay rate of the neutron that depends on QCD, using a numerical method called ‘lattice gauge theory' in which each point on a grid corresponds to a point in space-time. By solving the problem on successively finer grids, the calculations approach the true ‘continuum limit' of the real world. The state-of-the-art calculations were made possible through the use of the QCDOC supercomputers at Columbia University, the RIKEN BNL Research Center, and the University of Edinburgh.
Most implementations of lattice gauge theory correspond to three spatial dimensions and one time dimension, but Blum and his colleagues use a ‘mathematical trick' called ‘domain wall fermions'. They perform their calculations in four space dimensions—only reducing their answer back to the three-dimensional world at the end. The trick allows the group to capture important physics that most three-dimensional theories cannot.
An important aspect of the work lies in being able to test a sophisticated numerical technique that is consistent with the Standard Model and QCD against a simple result—neutron beta-decay. Confirmation that their results are accurate gives theorists the confidence to pursue increasingly complex problems in particle and nuclear physics.
Reference
1. Yamazaki, T., Aoki, Y., Blum, T., Lin, H.W., Lin, M. F., Ohta, S., Sasaki, S., Tweedie, R.J. & Zanotti, J.M. Nucleon axial charge in (2+1)-flavor dynamical-lattice QCD with domain-wall fermions. Physical Review Letters 100, 171602 (2008).
####
For more information, please click here
Copyright © Riken
If you have a comment, please Contact us.Issuers of news releases, not 7th Wave, Inc. or Nanotechnology Now, are solely responsible for the accuracy of the content.
| Related Links |
| Related News Press |
Physics
![]() Simulating magnetization in a Heisenberg quantum spin chain April 5th, 2024
Simulating magnetization in a Heisenberg quantum spin chain April 5th, 2024
News and information
![]() Simulating magnetization in a Heisenberg quantum spin chain April 5th, 2024
Simulating magnetization in a Heisenberg quantum spin chain April 5th, 2024
![]() NRL charters Navy’s quantum inertial navigation path to reduce drift April 5th, 2024
NRL charters Navy’s quantum inertial navigation path to reduce drift April 5th, 2024
![]() Discovery points path to flash-like memory for storing qubits: Rice find could hasten development of nonvolatile quantum memory April 5th, 2024
Discovery points path to flash-like memory for storing qubits: Rice find could hasten development of nonvolatile quantum memory April 5th, 2024
Discoveries
![]() Chemical reactions can scramble quantum information as well as black holes April 5th, 2024
Chemical reactions can scramble quantum information as well as black holes April 5th, 2024
![]() New micromaterial releases nanoparticles that selectively destroy cancer cells April 5th, 2024
New micromaterial releases nanoparticles that selectively destroy cancer cells April 5th, 2024
![]() Utilizing palladium for addressing contact issues of buried oxide thin film transistors April 5th, 2024
Utilizing palladium for addressing contact issues of buried oxide thin film transistors April 5th, 2024
Announcements
![]() NRL charters Navy’s quantum inertial navigation path to reduce drift April 5th, 2024
NRL charters Navy’s quantum inertial navigation path to reduce drift April 5th, 2024
![]() Discovery points path to flash-like memory for storing qubits: Rice find could hasten development of nonvolatile quantum memory April 5th, 2024
Discovery points path to flash-like memory for storing qubits: Rice find could hasten development of nonvolatile quantum memory April 5th, 2024
|
|
||
|
|
||
| The latest news from around the world, FREE | ||
|
|
||
|
|
||
| Premium Products | ||
|
|
||
|
Only the news you want to read!
Learn More |
||
|
|
||
|
Full-service, expert consulting
Learn More |
||
|
|
||








